My team got the 5th place which is out of our expectation, although we are 10 points away from getting a prize. Here’s the writeups for some challenges I found interesting.
Baby RSA
In short: just another implementation of the standard RSA algorithm. But instead of operating on the multiplicative group of integers modulo \(n\) (\(\Z^{\times}_n\)), it operates on the general linear group of 2x2 matrices (\(\mathrm{GL}_2(R)\)), over the ring of integers modulo \(n\) (\(\Z/n\Z\)), and matrix multiplication acts as the group operation. The flag is divided into 4 parts of equal length and are assembled into a 2x2 matrix:
\[C = M^e \mod n \]
where \(C, M \in \mathrm{GL}_2(\Z/n\Z)\). And as always, we’re given \(C\), \(e\), and \(n\). To clear up any confusion, the \(k\)th power of a matrix is defined as the matrix multiplied by itself \(k\) times.
Does the RSA decryption algorithm still work in this case? Recall that the correctness of RSA relies on Euler’s theorem:
\[ M^{\phi(n)} \equiv 1 \mod n \]
where \(\phi(n)\) is the Euler’s totient function.
The key is to notice that Euler’s theorem holds for any group \(G\) with \(|G|\) as the exponent, since it is a consequence of Lagrange’s theorem (the order of any subgroup divides \(|G|\)). In the everyday version of RSA, the group is \(\Z^{*}_n\) with \(|\Z^{*}_n| = \phi(n) = (p-1)(q-1)\). But since we’re working with a totally different group, \(|G|\) could be another number.
How do we figure out the order of the group \(\mathrm{GL}_2(\Z/n\Z)\)? Well, you can
either work it out yourself or look it up. I found this wikipedia entry
to be helpful: 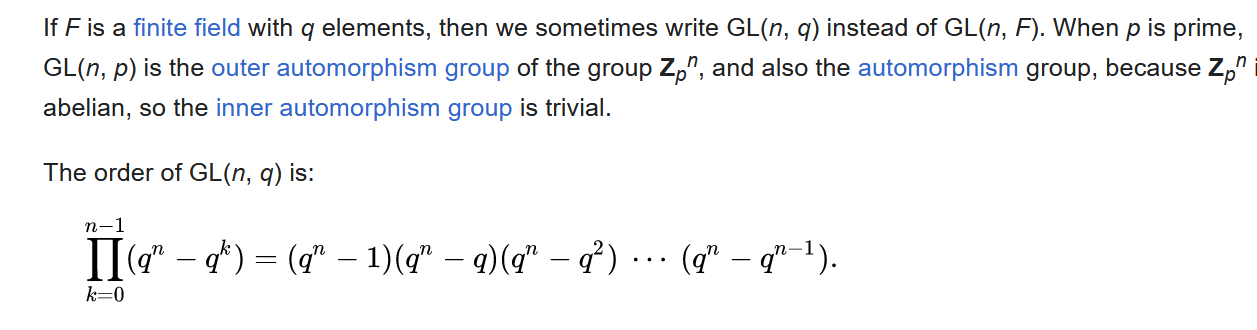 and
also this post:
and
also this post: 
Therefore we know that \[ |\mathrm{GL_2}(\Z/n\Z)| = |\mathrm{GL_2}(\Z/p\Z) \times \mathrm{GL_2}(\Z/q\Z)| = |\mathrm{GL_2}(\Z/p\Z)| \cdot |\mathrm{GL_2}(\Z/q\Z)| = (p^2 - 1)(p^2 - p)(q^2 - 1)(q^2 - q) \]
where \(p\) and \(q\) are the prime factors of \(n\).
Solution
- Factorize \(n\) into \(p\) and \(q\) with factordb
- Calculate the private exponent \(d = e^{-1} \mod |\mathrm{GL_2}(\Z/n\Z)|\), where \(|\mathrm{GL_2}(\Z/n\Z)| = (p^2 - 1)(p^2 - p)(q^2 - 1)(q^2 - q)\)
- Compute \(M = C^d \mod n\) and convert the 2x2 matrix into a string.
from sage.all import Zmod, matrix
N = 23036769723266886125458649758956702648712087220176816714653838673509877792118247880199359383510351312176460013557289096284919848198450380140055143077150138568183361851259869327791757963071569189728166204980100709764185330342160274626199317196467443629331873914435565361740711829939685538189329988893139409587357168398853766369829738504476214206419533085521724453948450717252383742145150063213519788568096297255648618658652421978414668802766216274568505191139490500068196963713850595634438745810451971497700218653640156817206666005050648173171079623763116133293956506581891112418298346805489471936353543559531981211007
p = 142753777417406810805072041989903711850167885799807517849278708651169396646976000865163313860950535511049508198208303464027395072922054180911222963584032655378369512823722235617080276310818723368812500206379762931650041566049091705857347865200497666530004056146401044724048482323535857808462375833056005919409
q = 161374151633887880567835370500866534479212949279686527346042474641768055324964720409600075821784325443977565511087794614167314642076253331252646071422351727785801273964216434051992658005517462757428567737089311219316483995316413254806332369908230656600378302043303884997949582553596892625743238461113701189423
m1 = 1688577118446994385968395107806136174557142107804975322078207849525996285555656260206580838013574154251970203340703172180307805295789863681283046955877515739613672185613439469419425659032767602825819847219860905891392664014905971901451235627837496286542641845303536183734346369265871928783878050715880767075204893640825827066572492472864317363779978890211475665989661613794835422235110473900325805989480105707322458100086102303069248435024193963568479630095651085817172713153787750186709036320119742855813602544679565063074620877551442333603722559931510193751993188654930045306930807753396090518988163885812861328189
m2 = 18606463074580041693118069235767195213344066322201243933010124107272334567447663310708859928135248241928811046109792797329702178779044479338641854986887585852036771229299545163561638784460129107079511967710507982185476509331836514884444253942126004228635338987949444364518676287270400269043532256579176612622679395079052278682848464034157076964064322042035138509130313802613501396522880243712216854338598648367312720616782393105428479703623071360086057689649365178333773145772588572015939657826398962685161288423080270520975839574982048787013451521127610126137432250909569570414617885182251535827422178518761878640277
m3 = 22650267491831158961493494945635419844978993992819562614030880303587890478134180756396307352921983637402503752225448743686715822967217573439050236903594508595369091970111469500428669690977435841418094876487761793949578523234589853571632054703229482334937567369737020238048709571084522258359213151775018534100702058932510299117617733363931262015526536137995495014561936341027015204484556877558726525974581334282869767778621415848776011642380798198145859047068171891683277816103814122546549427956819314641580598561780283977143766729878132075206011816915101647516926375041348314081517895281616142461484593652580056221170
m4 = 21918251154970082314222727740598056021059485736289135003915749232429908966741747423007921579944599958250485131086510119153324415101442340819161587864992420876845822880037498353379555319411381764829992580481479390290007103089320444053573660373539839479887140094345654253438765837610846183906780001563278053108924452477590722136992300951542317836042467648565676610116549645312286546804494679220834545780288823406596099528171318966103110446627459454678950065440952742712213009905322683034224640705258686542355943237539849218298957686667728849048771501755939158694731521586755665323051264657459810178627357183164938178482
def int_to_bytes(x: int) -> bytes:
return x.to_bytes((x.bit_length() + 7) // 8, 'big')
mat = matrix(Zmod(N), [[m1, m2], [m3, m4]])
e = 65537
d = pow(e, -1, (p**2-1)*(p**2-p)*(q**2-1)*(q**2-q))
dec = mat ** d
for col in dec:
for i in col:
print(int_to_bytes(int(i)).decode(), end='')Combinatorial Conundrum
We’re given a list of unknown integers \(x_1\), \(x_2\), …, \(x_{26}\), with a constraint \(a_i \lt x_i \leq b_i\) for each of them. The goal is to find the number of solutions \((x_1, x_2, ..., x_{26})\) to the equation \(x_1 + x_2 + \cdots + x_{26} = 69696969\).
There are a couple tricks to simplify this problem. The first thing I did is to substiture \(y_i\) for \(x_i - a_i\), and the equation becomes \(y_1 + y_2 + \cdots + y_{26} = 69696969 - (a_1 + a_2 + \cdots + a_{26})\). The constraints are then much easier to work with: \(0 \leq y_i \lt b_i - a_i\).
So is there a general formula for this problem? The closest I could find is when \(b_i - a_i\) is constant for all \(i\), but it is not at all the case here. Smells like a dynamic programming problem. (Please enlighten me if you know the name of this problem)
Let’s look at a simpler version of the problem: \(y_1 + y_2 + y_3 = 8\), with \(0 \leq y_1 \lt 4\) and \(0 \leq y_2 \lt 6\) and \(0 \leq y_3 \lt 5\). We can draw a table starting with \(y_1 + y_2\):

Simple right? The count \(C_1(s)\) of each sum \(s\) in the table increases for \(s < 4\), stays the same for \(4 \leq s \lt 6\), and decreases for \(s \geq 6\). Now what happens when we add \(y_3\)? each column of the table is now weighted by \(c_s\):
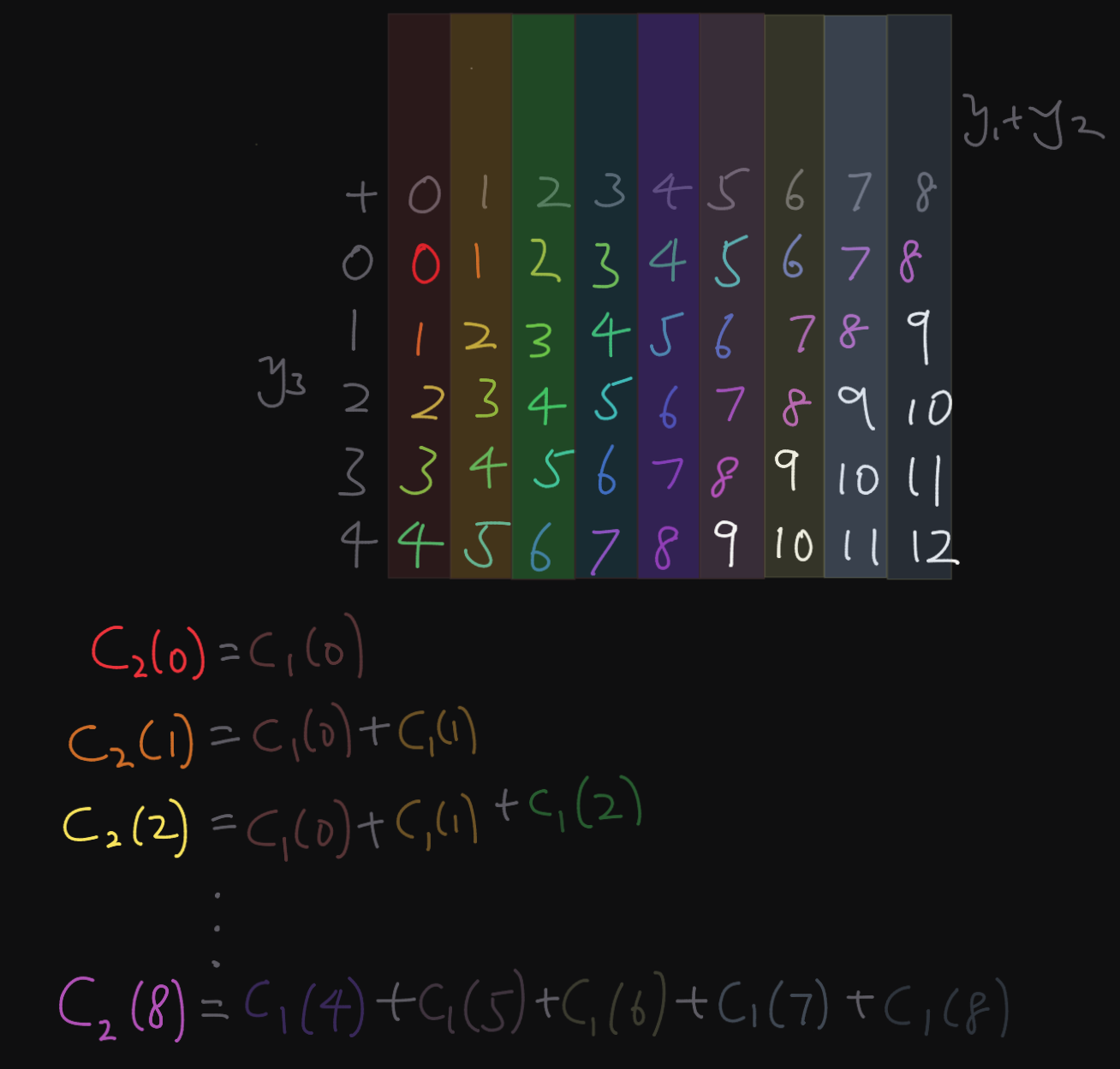
The number of solutions \(C_2(s)\) summing to \(s\) is now the sum of all \(C_1(k)\), where each column labeled \(k\) contains \(s\):
\[ C_2(s) = \begin{cases} C_2(0) & \text{if } s = 0 \\ C_2(s-1) + C_1(s) & \text{if } 0 \leq s < L_3 \\ C_2(s-1) + C_1(s) - C_1(s-L_3) & \text{if } L_3 \leq s < L_2 \\ C_2(s-1) - C_1(s-L_3) & \text{if } s \geq L_2 \\ \end{cases} \]
where \(0 \leq y_1 + y_2 < L_2 = 9\) and \(0 \leq y_3 < L_3 = 5\). Then \(C_2(8)\) is the number of solutions to \(y_1 + y_2 + y_3 = 8\). Keep in mind the formula asserts that \(L_2 \geq L_3\).
If we extend this to 26 variables, the general formula for obtaining \(C_{i+1}(s)\) from \(C_i(s)\) for \(0 < i < 26\) is pretty obvious. And to optimize the running time, the result of \(C_i(s)\) can be stored in an array to be used in the next iteration. The array could be trimmed to size \(69696969 - (a_1 + a_2 + \cdots + a_{26}) + 1\) since the values past it are not needed as they are too large for the sum.
Solution
lower_bounds = [
2008, 5828, 2933, 411, 4223, 1614, 5679, 6349, 117, 2321, 2281, 1939, 6273, 1477, 800, 4727, 2828, 1782, 1744, 2486, 6312, 2188, 5380, 1772, 2708, 1528
]
assert len(lower_bounds) == 26
upper_bounds = [
67434882, 35387831, 30133881, 63609725, 18566959, 25526751, 44298843, 26793895, 40292840, 42293336, 26301527, 50793633, 51546489, 36871159, 65314188, 15882817, 40562779, 48186923, 37382713, 56149154, 18170199, 63940428, 58244044, 29193116, 22309445, 40848052
]
assert len(upper_bounds) == 26
target = 69696969 - sum(lower_bounds)
bounds = [u - l for l, u in zip(lower_bounds, upper_bounds)]
bounds = sorted(bounds)
print(bounds)
assert len(bounds) == 26
def combs(target, bounds):
bounds = sorted(bounds, reverse=True)
prev_counts = [1] * bounds[0] + [0] * (target + 1 - bounds[0])
for n in range(1, len(bounds)):
print('n =', n, ', bound:', bounds[n])
counts = [0] * (target + 1)
for i in range(target + 1):
if i == 0:
counts[i] = prev_counts[0]
if i < bounds[n]:
counts[i] = counts[i - 1] + prev_counts[i]
else:
counts[i] = counts[i - 1] - \
prev_counts[i - bounds[n]] + prev_counts[i]
prev_counts = counts
return counts[target]
print('target:', target)
count = combs(target, bounds)
print(count )
print('Answer: ', count % 69696969)